2023年全国新高考Ⅰ卷高考数学试题【word精校版】

绝密★启用前
    

试卷类型：A
    

2023年普通高等学校招生全国统一考试（新高考全国Ⅰ卷）
    

数   学
 
    

本试卷共4页，22小题，满分150分.考试用时120分钟.
    

注意事项：
    

1．答题前，考生务必用黑色字迹钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写在答题卡上。用2B铅笔将试卷类型（A）填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.
    

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.
    

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.
    

4．考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回.
    

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
    

1. 已知集合，，则（    ）
    

A  B.  C.  D. 2
    

2. 已知，则（    ）
    

A  B.  C. 0 D. 1
    

3. 已知向量，若，则（    ）
    

A.  B.
    

C.  D.
    

4. 设函数在区间上单调递减，则的取值范围是（    ）
    

A.  B.
    

C  D.
    

5. 设椭圆的离心率分别为．若，则（    ）
    

A.  B.  C.  D.
    

6. 过点与圆相切的两条直线的夹角为，则（    ）
    

A. 1 B.  C.  D.
    

7. 记为数列的前项和，设甲：为等差数列；乙：为等差数列，则（    ）
    

A. 甲是乙的充分条件但不是必要条件
    

B. 甲是乙的必要条件但不是充分条件
    

C. 甲是乙的充要条件
    

D. 甲既不是乙的充分条件也不是乙的必要条件
    

8. 已知，则（    ）．
    

A.  B.  C.  D.
    

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分.
    

9. 有一组样本数据，其中是最小值，是最大值，则（    ）
    

A. 的平均数等于的平均数
    

B. 的中位数等于的中位数
    

C. 的标准差不小于的标准差
    

D. 的极差不大于的极差
    

10. 噪声污染问题越来越受到重视．用声压级来度量声音的强弱，定义声压级，其中常数是听觉下限阈值，是实际声压．下表为不同声源的声压级：
    

已知在距离燃油汽车、混合动力汽车、电动汽车处测得实际声压分别为，则（    ）．
    

A.  B.
    

C.  D.
    

11. 已知函数的定义域为，，则（    ）．
    

A.  B.
    

C. 是偶函数 D. 为的极小值点
    

12. 下列物体中，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度忽略不计）内的有（    ）
    

A. 直径为的球体
    

B. 所有棱长均为的四面体
    

C. 底面直径为，高为的圆柱体
    

D. 底面直径为，高为的圆柱体
    

三、填空题：本题共4小题，每小题5分，共20分．
    

13. 某学校开设了4门体育类选修课和4门艺术类选修课，学生需从这8门课中选修2门或3门课，并且每类选修课至少选修1门，则不同的选课方案共有________种（用数字作答）．
    

14. 在正四棱台中，，则该棱台的体积为________．
    

15. 已知函数在区间有且仅有3个零点，则的取值范围是________．
    

16. 已知双曲线的左、右焦点分别为．点在上，点在轴上，，则的离心率为________．
    

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．
    

17. 已知在中，．
    

（1）求；
    

（2）设，求边上的高．
    

18. 如图，正四棱柱中，．点分别在棱,上，．
    

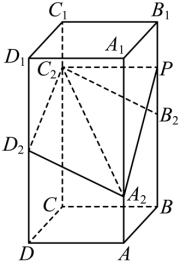
（1）证明：；
    

（2）点在棱上，当二面角时，求．
    

19. 已知函数．
    

（1）讨论的单调性；
    

（2）证明：当时，．
    

20. 设等差数列的公差为，且．令，记分别为数列的前项和．
    

（1）若，求的通项公式；
    

（2）若为等差数列，且，求．
    

21. 甲、乙两人投篮，每次由其中一人投篮，规则如下：若命中则此人继续投籃，若末命中则换为对方投篮．无论之前投篮情况如何，甲每次投篮的命中率均为0.6，乙每次投篮的命中率均为0.8．由抽签确定第1次投篮的人选，第1次投篮的人是甲、乙的概率各为0.5．
    

（1）求第2次投篮的人是乙的概率；
    

（2）求第次投篮的人是甲的概率；
    

（3）已知：若随机变量服从两点分布，且，
    

则．记前次（即从第1次到第次投篮）中甲投篮的次数为，求．
    

22. 在直角坐标系中，点到轴的距离等于点到点的距离，记动点的轨迹为．
    

（1）求的方程；
    

（2）已知矩形有三个顶点在上，证明：矩形的周长大于．