高中数学复数运算公式整理

复数
    

友情提醒：由于高三网站宽度限制，上传文本可能存在页面排版较乱的情况，如果点击下载或全屏查看效果更佳。查看本科目或其他科目更多知识点
    

考试内容：复数的概念；复数的加法和减法；复数的乘法和除法；数系的扩充。
    

复数知识要点：复数是高中代数的重要内容，在高考试题中约占8%-10%，一般的出一道基础题和一道中档题，经常与三角、解析几何、方程、不等式等知识综合.本章主要内容是复数的概念，复数的代数、几何、三角表示方法以及复数的运算.方程、方程组，数形结合，分域讨论，等价转化的数学思想与方法在本章中有突出的体现.而复数是代数，三角，解析几何知识，相互转化的枢纽，这对拓宽学生思路，提高学生解综合习题能力是有益的.数、式的运算和解方程，方程组，不等式是学好本章必须具有的基本技能.简化运算的意识也应进一步加强.
    

1.知识网络图
    

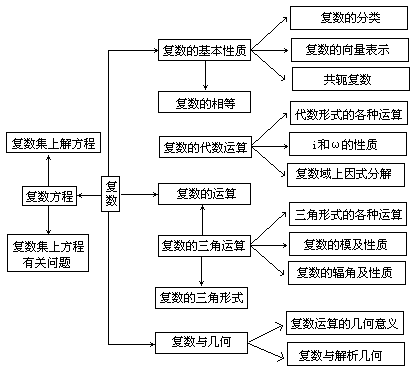
　　2.复数中的难点
    

　　(1)复数的向量表示法的运算.对于复数的向量表示有些学生掌握得不好，对向量的运算的几何意义的灵活掌握有一定的困难.对此应认真体会复数向量运算的几何意义，对其灵活地加以证明.
    

　　(2)复数三角形式的乘方和开方.有部分学生对运算法则知道，但对其灵活地运用有一定的困难，特别是开方运算，应对此认真地加以训练.
    

　　(3)复数的辐角主值的求法.
    

　　(4)利用复数的几何意义灵活地解决问题.复数可以用向量表示，同时复数的模和辐角都具有几何意义，对他们的理解和应用有一定难度，应认真加以体会.
    

　　3.复数中的重点
    

　　(1)理解好复数的概念，弄清实数、虚数、纯虚数的不同点.
    

　　(2)熟练掌握复数三种表示法，以及它们间的互化，并能准确地求出复数的模和辐角.复数有代数，向量和三角三种表示法.特别是代数形式和三角形式的互化，以及求复数的模和辐角在解决具体问题时经常用到，是一个重点内容.
    

　　(3)复数的三种表示法的各种运算，在运算中重视共轭复数以及模的有关性质.复数的运算是复数中的主要内容，掌握复数各种形式的运算，特别是复数运算的几何意义更是重点内容.
    

　　(4)复数集中一元二次方程和二项方程的解法.
    

4. ⑴复数的单位为i，它的平方等于－1，即.
    

⑵复数及其相关概念：
    

①   复数—形如a + bi的数（其中）；
    

②   实数—当b = 0时的复数a + bi，即a；
    

③   虚数—当时的复数a + bi；
    

④   纯虚数—当a = 0且时的复数a + bi，即bi.
    

⑤   复数a + bi的实部与虚部—a叫做复数的实部，b叫做虚部（注意a，b都是实数）
    

⑥   复数集C—全体复数的集合，一般用字母C表示.
    

⑶两个复数相等的定义：
    

.
    

⑷两个复数，如果不全是实数，就不能比较大小.
    

注：①若为复数，则若，则.（×）[为复数，而不是实数]
    

若，则.（√）
    

②若，则是的必要不充分条件.（当，
    

时，上式成立）
    

5. ⑴复平面内的两点间距离公式：.
    

其中是复平面内的两点所对应的复数，间的距离.
    

由上可得：复平面内以为圆心，为半径的圆的复数方程：.
    

⑵曲线方程的复数形式：
    

①为圆心，r为半径的圆的方程.
    

②表示线段的垂直平分线的方程.
    

③为焦点，长半轴长为a的椭圆的方程（若，此方程表示线段）.
    

④表示以为焦点，实半轴长为a的双曲线方程（若，此方程表示两条射线）.
    

⑶绝对值不等式：
    

设是不等于零的复数，则
    

①.
    

左边取等号的条件是，右边取等号的条件是.
    

②.
    

左边取等号的条件是，右边取等号的条件是.
    

注：.
    

6. 共轭复数的性质：
    

??????????????????????????????????????????
    

，（a + bi）??????????????
    

?????????????????????????????????
    

（）?????????????????????????????
    

注：两个共轭复数之差是纯虚数. （×）[之差可能为零，此时两个复数是相等的]
    

7 ⑴①复数的乘方：
    

②对任何，及有
    

③?
    

注：①以上结论不能拓展到分数指数幂的形式，否则会得到荒谬的结果，如若由就会得到的错误结论.
    

②在实数集成立的. 当为虚数时，，所以复数集内解方程不能采用两边平方法.
    

⑵常用的结论：
    

???
    

若是1的立方虚数根，即，则????????????????????????????????????????????????? .
    

8.? ⑴复数是实数及纯虚数的充要条件：
    

①.
    

②若，是纯虚数.
    

⑵模相等且方向相同的向量，不管它的起点在哪里，都认为是相等的，而相等的向量表示同一复数. 特例：零向量的方向是任意的，其模为零.
    

注：.
    

9. ⑴复数的三角形式：.
    

辐角主值：适合于0≤＜的值，记作.
    

注：①为零时，可取内任意值.
    

②辐角是多值的，都相差2的整数倍.
    

③设则.
    

⑵复数的代数形式与三角形式的互化：
    

，，.
    

⑶几类三角式的标准形式：
    

10. 复数集中解一元二次方程：
    

在复数集内解关于的一元二次方程时，应注意下述问题：
    

①当时，若＞0，则有二不等实数根；若=0，则有二相等实数根；若＜0，则有二相等复数根（为共轭复数）.
    

②当不全为实数时，不能用方程根的情况.
    

③不论为何复数，都可用求根公式求根，并且韦达定理也成立.
    

11. 复数的三角形式运算：
    

棣莫弗定理：