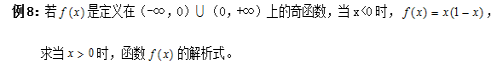高中数学如何判断函数的奇偶性

函数的奇偶性
    

友情提醒：由于高三网站宽度限制，上传文本可能存在页面排版较乱的情况，如果点击下载或全屏查看效果更佳。
    

知识点概述
    

1. 理解函数的奇偶性及其几何意义； 
    

2. 学会判断函数的奇偶性； 
    

3. 学会运用函数图象理解和研究函数的性质.
    

一、定义
    

对于函数f(x)，如果对于定义域内任意一个x，都有f(-x)=-f(x)，那么f(x)为奇函数;
    

对于函数f(x)，如果对于定义域内任意一个x，都有f(-x)=f(x)，那么f(x)为偶函数;
    

奇函数：关于原点对称。（做题时可考虑特殊值法），f（0）=0）。F（-x）= -f（x）
    

偶函数：关于y轴对称。F（-x）=f（x）
    

高三网小编为大家整理整理了高中语数外、政史地、物化生九科知识点，各科知识点都包含了知识专题、学习方法、解题技巧等内容。更多2016年高考各科复习知识点请查看<<<高中总站>>>( http://www.gaosan.com/zt/zhishidian.html#)，高考知识点频道有你想要的珍贵复习资料。欢迎访问高三网，高考生的专属网站。
    

二、函数f（x）的奇偶性
    

（1）如果对于函数定义域内的任意一个x，都有f（-x）=－f（x），那么函数f（x）就叫做奇函数。
    

（2）如果对于函数定义域内的任意一个x，都有f（-x）=f（x），那么函数f（x）就叫做偶函数。
    

（3）如果对于函数定义域内的任意一个x，f（-x）=-f（x）与f（-x）=f（x）同时成立，那么函数f（x）既是奇函数又是偶函数，称为既奇又偶函数。
    

（4）如果对于函数定义域内的任意一个x，f（-x）=-f（x）与f（-x）=f（x）都不能成立，那么函数f（x）既不是奇函数又不是偶函数，称为非奇非偶函数。
    

说明：①奇、偶性是函数的整体性质，对整个定义域而言
    

②奇、偶函数的定义域一定关于原点对称，如果一个函数的定义域不关于原点对称，则这个函数一定不是奇（或偶）函数。
    

（分析：判断函数的奇偶性，首先是检验其定义域是否关于原点对称，然后再严格按照奇、偶性的定义经过化简、整理、再与f（x）比较得出结论）
    

③判断或证明函数是否具有奇偶性的根据是定义
    

三、性质
    

　　(1)函数依据奇偶性分类可分为：奇函数非偶函数，偶函数非奇函数，既奇且偶函数，非奇非偶函数;
    

　　(2) f(x),g(x)的定义域为D;
    

　　(3)图象特点：奇函数的图象关于原点对称;偶函数的图象关于原点对称;
    

　　(4)定义域关于原点对称是函数具有奇偶性的必要不充分条件，奇函数f(x)在原点处有定义，则有f(0)=0;
    

　　(5)任意一个定义域关于原点对称的函数f(x)总可以表示为一个奇函数与偶函数的和的形式：f(x)=g(x)+h(x)，其中g(x)=-[f(x)+f(-x)]为偶函数，h(x)=-[f(x)-f(-x)]为奇函数;
    

　　(6)奇函数在关于原点对称的区间具有相同的单调性，偶函数在关于原点对称的区间具有相反的单调性。
    

四、奇偶函数图像的特征
    

定理奇函数的图像关于原点成中心对称图表，偶函数的图象关于y轴或轴对称图形。
    

f（x）为奇函数《＝＝》f（x）的图像关于原点对称
    

点（x，y）→（-x，-y）
    

奇函数在某一区间上单调递增，则在它的对称区间上也是单调递增。
    

偶函数在某一区间上单调递增，则在它的对称区间上单调递减。
    

五、奇偶函数运算
    

（1）两个偶函数相加所得的和为偶函数。
    

（2）两个奇函数相加所得的和为奇函数。
    

（3）一个偶函数与一个奇函数相加所得的和为非奇函数与非偶函数。
    

（4）两个偶函数相乘所得的积为偶函数。
    

（5）两个奇函数相乘所得的积为偶函数。
    

（6）一个偶函数与一个奇函数相乘所得的积为奇函数。
    

六、拓展延伸
    

　　(1)一般地，对于函数y=f(x)，定义域内每一个自变量x，都有f(a+x)=2b-f(a-x)，则y=f(x)的图象关于点(a,b)成中心对称;
    

　　(2)一般地，对于函数y=f(x)，定义域内每一个自变量x都有f(a+x)=f(a-x)，则它的图象关于x=a成轴对称。

利用函数的奇偶性求值

利用函数的奇偶性和单调性比较值的大小

利用奇偶性求函数解析式